The next is an article (2001) where the percentage of the funds risked and the leverage of a position is calculated from the volatility and the average duration of the position. It is applied on the futures on indexes of the Arhens Derivatives Exchange (ADEX).
Initial Remark: We must be aware that the academic research has accepted and published nay different and often contradictory statistical or probabilistic models of the market, the trend of the market and generally its patterns of moves. Statistical results are very sensitive to the way we handle the sampling over the same market. And each research focuses and handles the sampling of the market in different ways. It requires special and wise scientific analysis of the sampling to deduce really sound conclusions that are safe to let us put large amounts of money funds and capital. The continuous time geometric Brownian motion is a rather awkward model for the trend of the markets, because we have measured the Pareto distribution rather than log-normal distribution of the trend of prices , and due to the Pareto modeled inequalities of the enterprises and their inherited in the markets packets of orders, as we have mentioned in post 25 , 10 etc. Another difficulty is that it is continuous time model and its statistics even on minutes bars time frames or tick-wise is only approximate. In particular it is a model with much more risk than the actual of the trend in the markets. Still after the Black-Scholes model of option pricing (see e.g. https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model) , that resulted to a Nobel prize, it is standard in academic research to model the trend of the market with a continuous time geometric Brownian motion. In such models if r is less than (1/2) * s^2 then it is almost certain (in other words with probability equal to 1 ) that given sufficient time the path of the trend will get bankrupt that is it will return to the initial point! As also the ratio r/s^2 is the optimal exposure and adjustment from deductions of the same theory of ITO calculus (see the book "Stochastic Differential equations" by B. K. Oksendal (Springer editions) page 223, example 11.5 ) then this means that we are led to bankruptcy if the optimal exposure has to be less than 50% ! Other standard also discrete time models of exponential trend of the form y(n)=exp(rt(n))+e(n) with variance(e(n)=s and average(e(n))=0 do not have this bankruptcy property even if r is less than (1/2) * s^2 . It seems to me that such a continuous time model might be approximately acceptable , but still with many deviations from the reality , for very-very large samples of period measurements (bars or candlesticks) and only for instruments and time periods with very clear stable trend. If we assume this continuous time model of the trend as acceptable , then the next is an acceptable method of estimation of the required liquidity in buy and hold positions of futures.
Initial Remark: We must be aware that the academic research has accepted and published nay different and often contradictory statistical or probabilistic models of the market, the trend of the market and generally its patterns of moves. Statistical results are very sensitive to the way we handle the sampling over the same market. And each research focuses and handles the sampling of the market in different ways. It requires special and wise scientific analysis of the sampling to deduce really sound conclusions that are safe to let us put large amounts of money funds and capital. The continuous time geometric Brownian motion is a rather awkward model for the trend of the markets, because we have measured the Pareto distribution rather than log-normal distribution of the trend of prices , and due to the Pareto modeled inequalities of the enterprises and their inherited in the markets packets of orders, as we have mentioned in post 25 , 10 etc. Another difficulty is that it is continuous time model and its statistics even on minutes bars time frames or tick-wise is only approximate. In particular it is a model with much more risk than the actual of the trend in the markets. Still after the Black-Scholes model of option pricing (see e.g. https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model) , that resulted to a Nobel prize, it is standard in academic research to model the trend of the market with a continuous time geometric Brownian motion. In such models if r is less than (1/2) * s^2 then it is almost certain (in other words with probability equal to 1 ) that given sufficient time the path of the trend will get bankrupt that is it will return to the initial point! As also the ratio r/s^2 is the optimal exposure and adjustment from deductions of the same theory of ITO calculus (see the book "Stochastic Differential equations" by B. K. Oksendal (Springer editions) page 223, example 11.5 ) then this means that we are led to bankruptcy if the optimal exposure has to be less than 50% ! Other standard also discrete time models of exponential trend of the form y(n)=exp(rt(n))+e(n) with variance(e(n)=s and average(e(n))=0 do not have this bankruptcy property even if r is less than (1/2) * s^2 . It seems to me that such a continuous time model might be approximately acceptable , but still with many deviations from the reality , for very-very large samples of period measurements (bars or candlesticks) and only for instruments and time periods with very clear stable trend. If we assume this continuous time model of the trend as acceptable , then the next is an acceptable method of estimation of the required liquidity in buy and hold positions of futures.
ESTIMATION OF REQUIRED LIQUIDITY FOR INVESTMENT POSITION
IN FUTURES OF THE ATHENS
By Dr COSTAS KYRITSIS
Department of Mathematics
and Computer Science
Software Laboratory
of Athens 2001
Abstract
In this paper we discuss the risk of mark-to-market loss of positions with leverage, in futures. We make the usual assumptions of Lognormal distribution and geometric Brownian motion for the underlying as in the Black-Scholes options pricing model. With these assumptions we estimate tables of required liquidity for futures on FTSE-20 and FTSE-40 in the Athens Derivative Exchange Market, during the year 2000.
Key words
Derivatives, Geometric Brownian Motion, Stochastic Differential Equations, Simulation, Investment, Liquidity
§1 Introduction Since August 1999 the Athens Derivative Exchange Market (ADEX) introduced for the first time futures on the Index FTSE-20, and soon afterwards on the Index FTSE-40. At present the average amount of money that is traded in ADEX is 10-15 billion drachmas that is almost 3% of the traded money in the Athens Stock Exchange Market (ASE, October 2000). The interest is increasing with the introduction of options and stock lending. Nevertheless the peculiarities and risks of investing to futures are not quite clear to the present average investor. For example it is highly risky and not advisable to leave investment positions of futures that have loss till the market has reverse trend and they became profitable, as is done with securities. There is the risk of running out of the budget and eventually closing the position before it becomes profitable. In this paper we analyze the source of this risk and we estimate the required amount of money that should be kept in cash, for probable losses.
§2 Leverage in positions on futures
When investing in positions on futures we do not pay all the money of the investment.
Instead it is calculated daily the profit or loss of the investment position (called mark-to-market) and is paid by the investors and Broker Companies to appropriate clearance bank (Alpha Credit Bank). In addition it is paid a percentage only of the height of the position, as much as it is considered it is risked for 1-2 days for ADEX to close the position if anything goes wrong (default position). The percentage is estimated according to the volatility (standard deviation) of the daily percentage changes of the underlying Index and is called Margin . This percentage at present is 12% for futures on the Index FTSE-20 and 16% for futures on the Index FTSE-40. This makes an advantage for the investor as he must only pay 12%-16% of the height of a position when he opens it. This is called the leverage of the position and is a multiplier of 1/12%=8.33 times and 1/16%=6.25 times respectively. Of course not only the rate of return is multiplied with this numbers but also the Beta (or Elasticity) of the position. The advantage of leverage has also its risks , as the profit or loss is paid daily on 100% of the height of the position and in a reverse trend of the market can easily lead to bankruptcy, something not really possible with investment positions in securities.
§3 Volatility of the price of the underlying .
In order to estimate the required Liquidity we need a forecasting of the underlying Index for the investment horizon, and the correlation and coupling of the future with the underlying Index .
The most difficult parameter is that of the Market, in other words the forecasting of the Index. This obviously depends on the season and the particular trend of the market at the Investment time.
We shall go around this difficulty in a way that is standard in the pricing of Derivatives and is also used by ADEX in the estimation of the percentages of 12% and 16% for the margin. We shall assume a neutral market, neither growing neither decaying, but with a trend equal to the risk free rate (5.59% in a year base, at present October 2000). So the model of the underlying index is, as in the Black-Scholes option pricing model ,a Geometric Brownian Motion (continuous time random compound interest) of normally distributed rate r and volatility σ. .For the definition of the stochastic differential equations and the geometric Brownian motion see Oksental p121 Chpt. V p 60 ,exerc.7.9 ,p 121,example 5.1 p 60
The stochastic differential equation of Brownian motion (Ito interpretation) is:
The exact interpretation of the symbols requires the concepts and definitions of stochastic Integrals and is outside the scope of this paper. For the definitions see Oksental 1995.
The distribution of the prices Xt is Lognormal.
The solution of this stochastic differential equation is given by the formula:
where Bt is a Brownian Motion
The logarithm of this process Xt/ X0 is an ordinary Brownian motion with drift:
log(Xt/ X0)=(r-(1/2) s2)t + s Bt . (3)
The average time T that it reaches X for the first time starting from x0
Is T=log(X/ x0)/(r-(1/2) s2) (4)
If β is the beta (elasticity) of the future Yt over the index Xt we assume that the futures also, follows the equation
If l is the leverage of the investment the value of the investment position on the future follwos actually the equation
The conditional variance of the Index price Xt is calculated to have the formula
(see Karlin S-Taylor H.M.(1975) p 357)
Var(X(t)/X(0)=X0 )=X2Exp(2t(r+σ2/2))*(Exp(tσ2)-1) (7)
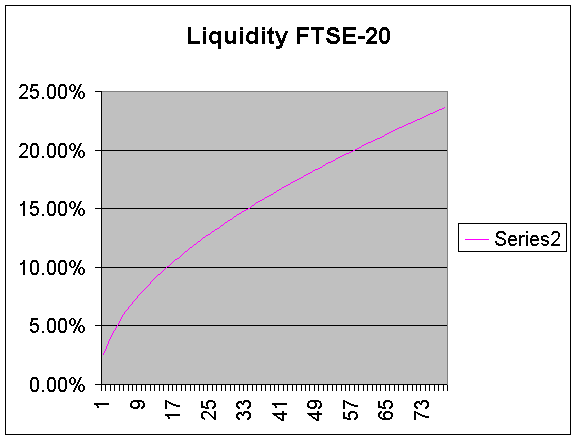
§4 Required Liquidity tables .
For the required liquidity of position of horizon t we may take the conditional volatility (standard deviation) of the price of the future .We should not forget that these formulas assume a neutral market and the liquidity is the average and not a worse scenario.
From the above formulae and assuming β=1 ,r=5.59% ,σ=40% (historic volatility of 1 year) for the FTSE-20 and σ=47% for the FTSE-40 (values that are used by ADEX at present and are estimated by the daily data) we compute the next tables.
Days-FTSE-20
|
Liquidity Percentage
|
Days-FTSE-20
|
Liquidity Percentage
|
Days-FTSE-20
|
Liquidity Percentage
|
Days-FTSE-20
|
Liquidity Percentage
|
1
|
2.53%
|
21
|
11.77%
|
41
|
16.68%
|
61
|
20.65%
|
2
|
3.58%
|
22
|
12.06%
|
42
|
16.90%
|
62
|
20.83%
|
3
|
4.39%
|
23
|
12.34%
|
43
|
17.11%
|
63
|
21.01%
|
4
|
5.07%
|
24
|
12.61%
|
44
|
17.32%
|
64
|
21.19%
|
5
|
5.68%
|
25
|
12.88%
|
45
|
17.53%
|
65
|
21.37%
|
6
|
6.22%
|
26
|
13.14%
|
46
|
17.74%
|
66
|
21.55%
|
7
|
6.73%
|
27
|
13.40%
|
47
|
17.94%
|
67
|
21.73%
|
8
|
7.20%
|
28
|
13.66%
|
48
|
18.14%
|
68
|
21.91%
|
9
|
7.64%
|
29
|
13.91%
|
49
|
18.35%
|
69
|
22.09%
|
10
|
8.06%
|
30
|
14.16%
|
50
|
18.54%
|
70
|
22.26%
|
11
|
8.46%
|
31
|
14.40%
|
51
|
18.74%
|
71
|
22.44%
|
12
|
8.84%
|
32
|
14.64%
|
52
|
18.94%
|
72
|
22.61%
|
13
|
9.21%
|
33
|
14.88%
|
53
|
19.13%
|
73
|
22.78%
|
14
|
9.56%
|
34
|
15.12%
|
54
|
19.33%
|
74
|
22.95%
|
15
|
9.90%
|
35
|
15.35%
|
55
|
19.52%
|
75
|
23.13%
|
16
|
10.24%
|
36
|
15.58%
|
56
|
19.71%
|
76
|
23.30%
|
17
|
10.56%
|
37
|
15.80%
|
57
|
19.90%
|
77
|
23.47%
|
18
|
10.87%
|
38
|
16.03%
|
58
|
20.09%
|
78
|
23.63%
|
19
|
11.18%
|
39
|
16.25%
|
59
|
20.28%
| ||
20
|
11.48%
|
40
|
16.47%
|
60
|
20.46%
|
Days/FTSE-40
|
Liquidity Percentage
|
Days/FTSE-40
|
Liquidity Percentage
|
Days/FTSE-40
|
Liquidity Percentage
|
Days/FTSE-40
|
Liquidity Percentage
|
1
|
2.98%
|
21
|
13.88%
|
41
|
19.75%
|
61
|
24.53%
|
2
|
4.21%
|
22
|
14.22%
|
42
|
20.01%
|
62
|
24.75%
|
3
|
5.16%
|
23
|
14.56%
|
43
|
20.26%
|
63
|
24.98%
|
4
|
5.97%
|
24
|
14.88%
|
44
|
20.52%
|
64
|
25.20%
|
5
|
6.68%
|
25
|
15.20%
|
45
|
20.77%
|
65
|
25.42%
|
6
|
7.32%
|
26
|
15.52%
|
46
|
21.02%
|
66
|
25.63%
|
7
|
7.91%
|
27
|
15.83%
|
47
|
21.26%
|
67
|
25.85%
|
8
|
8.47%
|
28
|
16.13%
|
48
|
21.51%
|
68
|
26.07%
|
9
|
8.99%
|
29
|
16.43%
|
49
|
21.75%
|
69
|
26.28%
|
10
|
9.49%
|
30
|
16.73%
|
50
|
21.99%
|
70
|
26.49%
|
11
|
9.96%
|
31
|
17.02%
|
51
|
22.23%
|
71
|
26.71%
|
12
|
10.41%
|
32
|
17.31%
|
52
|
22.47%
|
72
|
26.92%
|
13
|
10.84%
|
33
|
17.59%
|
53
|
22.70%
|
73
|
27.13%
|
14
|
11.26%
|
34
|
17.87%
|
54
|
22.94%
|
74
|
27.34%
|
15
|
11.67%
|
35
|
18.15%
|
55
|
23.17%
|
75
|
27.55%
|
16
|
12.06%
|
36
|
18.42%
|
56
|
23.40%
|
76
|
27.76%
|
17
|
12.45%
|
37
|
18.70%
|
57
|
23.63%
|
77
|
27.96%
|
18
|
12.82%
|
38
|
18.96%
|
58
|
23.86%
|
78
|
28.17%
|
19
|
13.18%
|
39
|
19.23%
|
59
|
24.08%
| ||
20
|
13.54%
|
40
|
19.49%
|
60
|
24.31%
|
Bibliography
Azariadis C.(1993) Intertemporal Macroeconomics Blackwell
Black F.Scholes M.(1976) The pricing of Options and Corporate Liabilities Journal of Economic Theory 10 pp 239-257
Broer D.P.-Jansen W.J.(1998) Dynamic Portfolio Adjustment and Capital
Controls: An Euler Equation Approach Southern Economic Journal 64(4) pp 902-921 .
Gencay R.(1998) Optimization of technical trading strategies and the profitability
in security markets.Economic Letters 59 pp249-254.
Elton E.J.-Gruber M.J. (1991) Modern portfolio theory and investment
analysis Wiley.
Elliot,R.N. (1980) The major workd of R.N. Elliot ,Chappaqua
(edited by Robert Prechter) NY:New Classics Library .
Kloeden E.P.-Platen E.-Schurtz h.(1997) Numerical Solutions of SDE
Through Computer Experiments Springer
Karlin S-Taylor H.M.(1975) A first course in stochastic processes. Academic press .
Magee J.(1992) Technical Analysis of Stock Trends New York Institute of Finance
Mallaris A.G.-Brock W.A.(1982) Stochastic Methods in Economics and
Finance North-Holland
Merton R.C (1968) Lifetime portfolio selection under uncertainty:The
continuous time case. Rev. Econ.Statist. II pp247-257
Mertzanis Ch.(1998) Limit of prices and variance of the general index in the
Millionis A.E..-Moschos D.(1998) Information Efficiency and application in
the Athens Institute of Statistics
Murphy J.J. Technical Analysis of the Futures Markets .New York
Oksendal B (1995) Stochastic Differential equations Springer 1995
Papadamoy S.-Papanastasiou D.-Tsopoglo (1998) Research on the predictability
of the stocks in the Athens Stockmarket. Proceedings of the Conference of the Institute of Statistics
Roy S.(1995) Theory of dynamic choice for survival under uncertainty
Mathematics of social sciences 30 pp171-194
Spanoudaki J.-Kampaneloy A.-Antonogiorkakis P.(1998) Volume indices in
the Technical analysis of stocks.Monte-Carlo empirical results. Proceedings of the Conference of the Institute of Statistics
Samuelson P.A.(1968) Lifetime portfolio selection by dynamic programming
Rev. Econ.Statist. II pp239-246